In another example of cutting-edge experiments that deserve recognition, Joerg Panzer (R&D TEAM, Germany) and Patrick Macey (PACSYS, UK) detail an investigation of the sound pressure response and radiation impedance of a loudspeaker horn driven by an electro-dynamic transducer. The two authors (and creators of the respective software tools) combined measurements with simulation software using finite and boundary element methods and explored the associated issues with meshing for each method.
The modeling of the frequency response of a given horn was the starting point for this experiment. Our curiosity focused on the results of the simulation software used and how the two different programs would compare, as well as how they correlate with the measured directivity and other performance metrics.
Simulation tools were used to solve the wave-equation in the frequency domain for given boundary conditions. As a result, we could obtain observations of the sound pressure response and the radiation impedance.
To understand the performance of the horn, independent of its environment and without any contribution from diffraction of baffle edges and room acoustic effects, it is informative to study its performance when it is mounted in an infinite rigid baffle and radiating into a half space.
For comparison of the calculation results, we selected two quantities. First, the lumped acoustic radiation impedance at the throat of the waveguide. Second, the sound pressure level (SPL) at a certain fixed distance at various angles in front of the baffle.
The lumped acoustic radiation impedance is notoriously difficult to measure. However, it is straightforward to extract from a simulation model. The radiation impedance is an important parameter for the design of a waveguide because the radiated power is proportional to the radiation resistance. Further, its curves are ideal candidates when it comes to comparing the results of simulation software. This is because the calculation of the lumped radiation impedance involves the whole acoustic field as an integral value.
The reason why we selected the sound pressure is that it is easily reproduced by calculation, and also because we had available the measurement device for taking directivity sound pressure measurements.
The Waveguide
The device under test is a little horn or waveguide with a mouth width and height of 95mm×95mm, a throat diameter of 12.7mm and a length of 170mm. Figure 1 shows a sketch of the view into the mouth of the waveguide, a cut of the view of the curved sides, and a cut of the view of the linear sides.
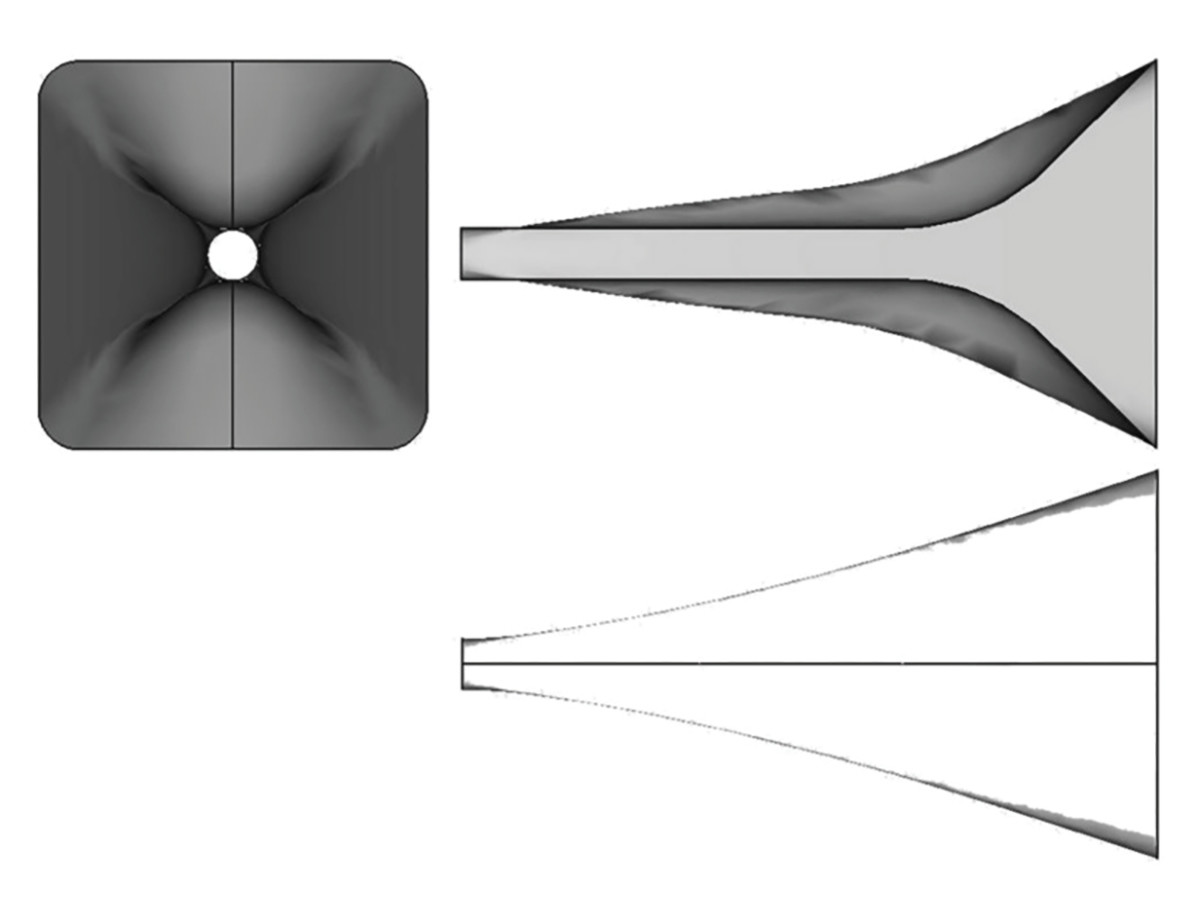
The flair of the horn does not follow any particular mathematical function. It has been designed with the help of a CAD tool. Basically, the waveguide opens linearly with a slight curvature in the first quarter along the horn. Additionally, there is a bump on two opposite sides yielding a constriction along the center of the horn.
Lumped Acoustic Radiation Impedance
During development of a waveguide for a loudspeaker, the designer typically has a close look at the curve of the lumped acoustic radiation impedance. This is because the acoustic output power of the horn is proportional to the real part of this impedance.
Hence, the variations of the impedance curve will inevitably have an effect on the sound quality of the speaker. When we speak here of the radiation impedance we mean the lumped acoustic impedance of the piston mode at the throat:
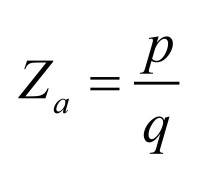
(1)
with volume velocity q=v×Sth and sound pressure p. We assume here that the acoustic velocity v is constant (pistonic) over the cross-sectional area of the throat Sth and points in the same direction. In Equation 1 the sound pressure is thought to be a mean value over Sth. A plausible mean-value can be obtained with the help of the acoustic power, which is in general:
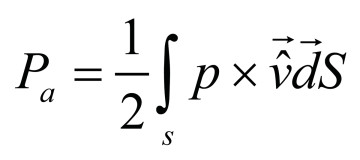
(2)
here, the factor “½” comes from the crest-factor of a sinusoidal wave where we assume p and v to be peak values of a sinusoidal signal. The acoustic velocity is a vector and we take the conjugate complex value. S can be any area. Then Pa is the acoustic power through that area.
If we combine Equation 1 and Equation 2 under the assumptions of uniform velocity (pistonic, v = 1) and S being the cross-section at the throat, then this will yield for the radiation impedance:
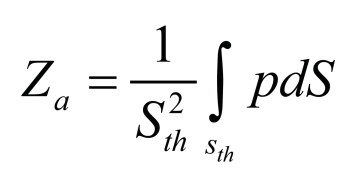
(3)
hence, the lumped radiation impedance at the throat would be proportional to the mean-value of the pressure, if the horn is excited by a uniform acoustic velocity.
This condition can be easily satisfied inside a simulation algorithm. However, for a measurement the uniform velocity condition would be more difficult to achieve, especially at frequencies where the wavelength is small compared to the dimension of the throat.
Having available the impedance Za one can calculate the acoustic power of the piston mode of the horn. Its real part is proportional to the acoustic power radiated into the far-field:
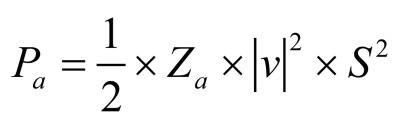
(4)
One can show that the lumped acoustic radiation impedance approaches always a certain value asymptotically at high frequencies, which is:
(5)
Equation 5 can be used to normalize the radiation impedance, so that the real part of any curve would approach the value of one at high frequencies. The imaginary goes to zero.
Figure 2 shows the result of the calculation of Equation 3. Displayed is the real part of the normalized lumped radiation impedance at the throat of the horn if excited by uniform driving velocity (piston-mode). The normalization is done by applying Equation 5, hence the curves should approach the value of one at high frequencies. The curves of Figure 2 can be regarded as a transmission characteristic and have a high-pass character.
The stop-band is at low frequencies below approximately 500Hz. At high frequencies the radiated power will follow the spectrum curve of the velocity at the throat. Between 500Hz and 3kHz the horn radiates selectively. For example, at 900Hz the radiated sound power would be more than twice that at high frequencies. At 1.2kHz the transmission is strongly attenuated. These fluctuations could be altered by changing the horn geometry.
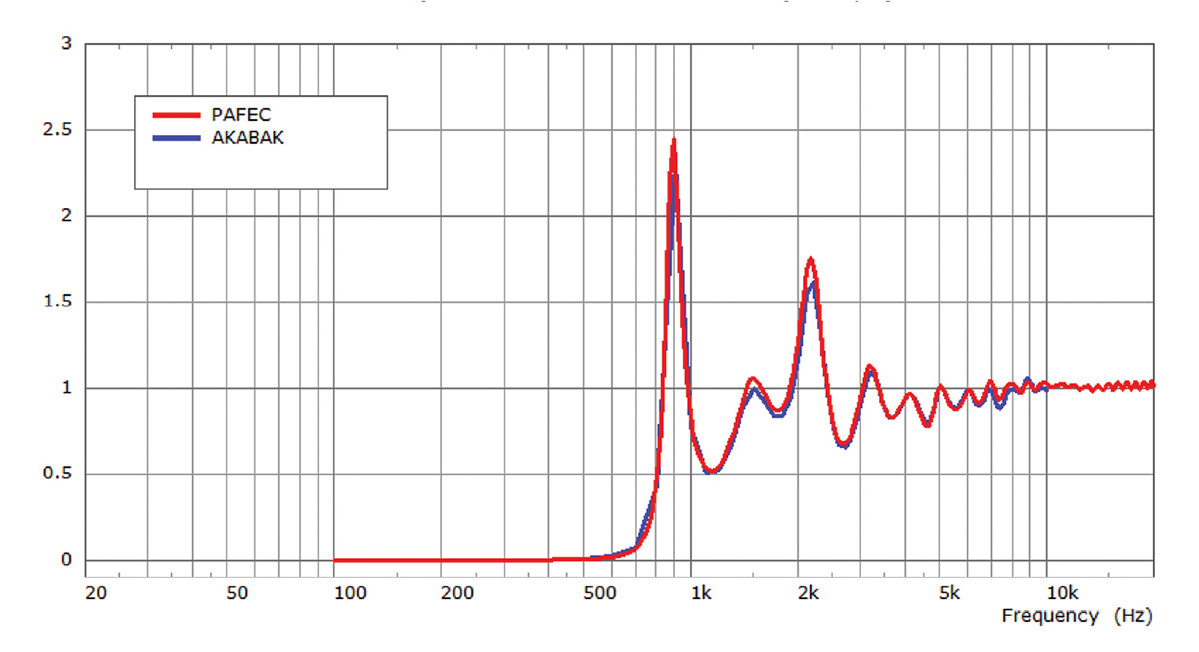
In this article we want to draw attention to the fact that there are two curves, which are almost identical. The red curve is the result of the PAFEC-simulator whereas the blue curve results from the AKABAK-simulator. These two software tools calculate the same response of the device under test. Their results are almost identical although the internal workings of these applications are different.
Measurements
For the measurement of the directivity, the horn is driven by a compression driver. The exit of its phase plug has a diameter of 12.7mm, which fits perfectly to the throat diameter of the waveguide. We focused on the normalized directivity. The normalization hides the influence of the properties of the driver. Hence, there is no need to describe the compression driver in detail. The response is linear because adjusting the drive voltage did not affect the directivity pattern.
The horn is fitted into a rotatable baffle of 910mm×600mm as shown in Photo 1. The directivity is the sound pressure in the far field at various positions of equal distance between the microphone and the center of the mouth. The distance of the microphone is d = 700mm. The baffle is rotated in the horizontal plane in 5-degree steps. The other dimension of rotation comes from a rotation about the on-axis. In this way a whole “balloon directivity measurement” could be performed. However, for this experiment we regard only the polar measurement of the horizontal plane (azimuth = 0 degrees) and of the vertical plane (azimuth = 90 degrees).
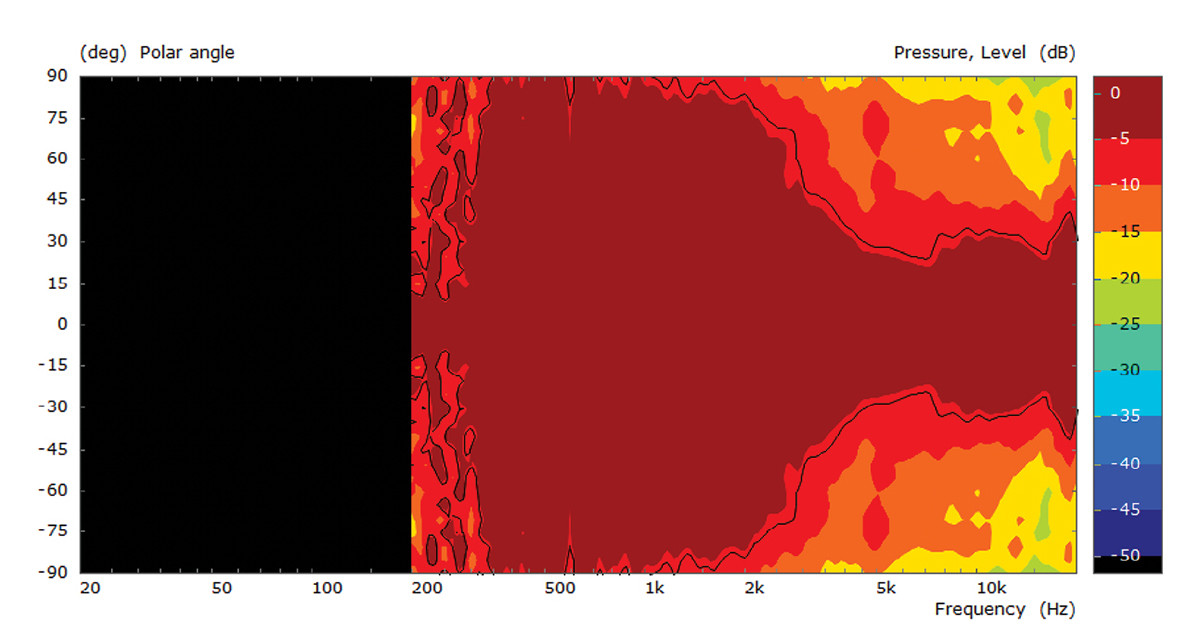
Figure 3 displays the measurement of normalized sound pressure level (SPL) taken at 19 microphone positions in a regular angular range between 0 degrees to 90 degrees. The map is mirrored to display the whole range from -90 degrees to 90 degrees. The colored contours range from -50dB to 0dB. For normalization each spectrum of the sound pressure is divided by the spectrum in an on-axis direction (0 degrees). The fine outline displays the contour at -6dB, which is also called the beamwidth curve. At low frequencies, the horn should radiate almost omni-directional. The slight deviations are caused by diffraction of the finite baffle and other insufficiency of the measurement situation.
Figure 4 shows the directivity in the vertical plane. In comparing the plot to the one of Figure 3, it is obvious that the beamwidth is broader. This is likely caused by the smaller aperture due to the bumps inside the horn.
Comparison of Directivity Calculations
Both simulation applications can calculate the sound pressure at the same locations as used for the measurement. The virtual microphone is placed at constant distance (d = 700mm) from the center of the horn mouth. Starting at the on-axis direction calculations are done at various angles in the horizontal and vertical planes. The angular distance between the positions is 5 degrees.
Figure 5 shows the angular distribution of the SPL in the horizontal plane. The polar plot shows curves at 2kHz, 5kHz, and 8kHz. At 2kHz the horn radiates almost omni-directional. At 5kHz beam-forming starts. At 8kHz radiation to the side is attenuated and most energy is radiated on-axis. The red curve is the result of the PAFEC-simulator, and the blue curve is the result of the AKABAK-simulator. The plot demonstrates the similarity of the calculation results.
Figure 6 shows the overlay of the simulated curves in the vertical plane. The broader pattern is caused by the bump, which yields a constricted aperture.
Comparison of Measurements and Simulation
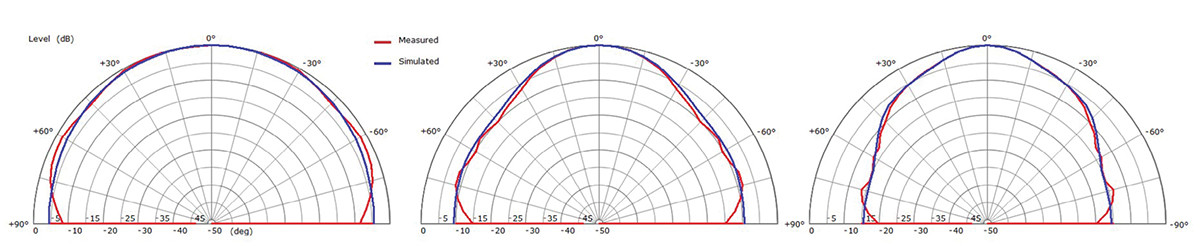
Figure 7 demonstrates an overlay of simulated and measured directivity curves in the horizontal plane and which curves are predominantly caused by the linear walls of the horn.
Figure 8 shows an overlay of simulated and measured curves in the vertical plane. There is a good agreement between the simulated and the measured results. The deviations close to 90 degrees are due to the fact that for the measurement the infinite baffle is finite after all.
Modeling for Simulation
The horn is mounted with its mouth flush in an infinite baffle. The infinite baffle is reflecting, and its boundary condition means that the component of the acoustic velocity, which is normal to its plane should be zero everywhere. The Sommerfeld radiation condition must be satisfied, to ensure that the pressure field in the half space consists of outgoing waves.
Simulation Methods and Subdomain Modeling
Many simulation methods are used in acoustics including finite difference, finite volume, finite element method (FEM) and boundary element method (BEM). In these experiments, FEM and BEM simulations are used. Each of these methods has strengths and weaknesses and it is consequently sometimes beneficial to split the acoustic domain into subdomains.
Two such decompositions are shown in Figure 9. Finite difference and finite volume approaches are obtained directly from the Helmholtz equation, using differencing operations to approximate derivatives. The FEM is also closely related to the underlying differential equation, which is multiplied by a weighting function and integrated by parts. The domain is decomposed into small elements such that the pressure can be assumed to vary as a linear combination of some suitable basis functions (e.g., low-order polynomials), within each element. Applying the Galerkin method produces the FEM linear equations.
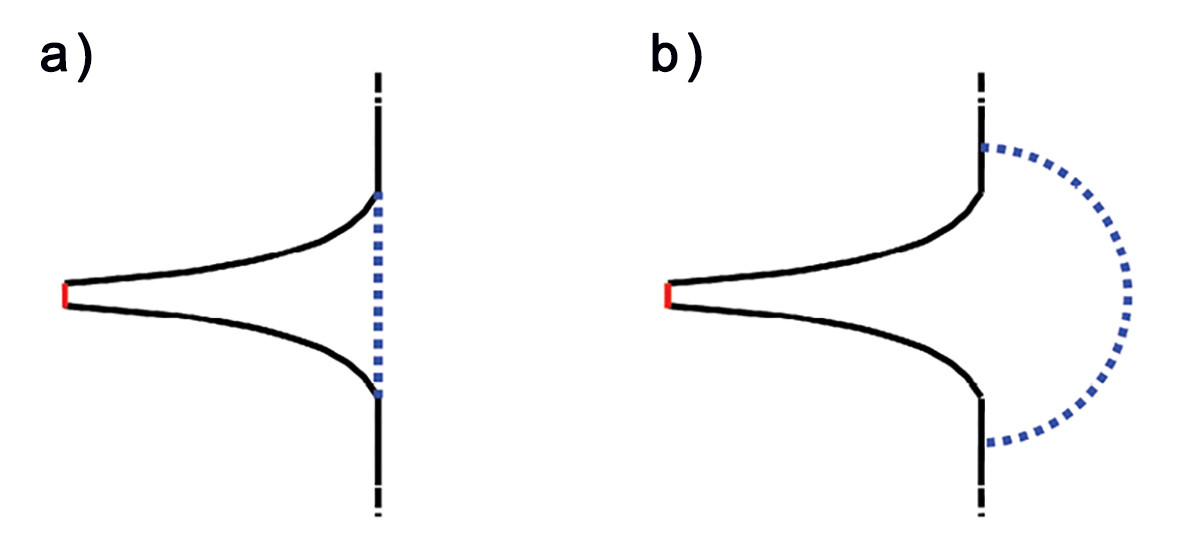
The BEM attempts to solve a derived integral equation, using a set of local basis functions on the bounding surface of the acoustic volume; within the domain itself the solution of the Helmholtz equation is ensured by the properties of the Green’s function. Only FEM and BEM are considered further, as they are used for the results in this article, see also for example [1, 2]. Both methods produce a set of linear equations, which are solved to determine the pressure at the nodes in the model. For FEM a large set of sparse equations are produced, as nodes are required on elements throughout the volume. For BEM a smaller dense set of equations is produced from the nodes on the surface elements. In both cases the element size has to be small enough to adequately represent the pressure variation, which in turn is usually related to the acoustic wavelength. Analysis at higher frequencies requires smaller elements, more nodes and hence has greater computational requirements: CPU time, memory, and disk space.
The surface of the horn has a sharp fold, particularly near the throat, such that the radius of curvature is smaller than the element side-length, which is needed from frequency-based considerations. This creates a concern that the geometry may not be adequately represented, which can be checked using mesh convergence.
The geometry and boundary conditions of the idealized problem have two planes of symmetry. It is possible to reduce the problem size by using a quarter model. All the simulations were using quarter models.
AKABAK
The AKABAK simulator [3] calculates the acoustic field inside the horn and in front of the baffle with the help of the boundary element method. The calculation of the Helmholtz Integral is usually a two-stage process. First, one has to solve for certain unknown parameters of the integral. If available, one can commence with the calculation of the observation points. To solve for the unknown parameters, one divides the surface of the acoustic boundary into small elements. Typically, the mesh-density needs to be found experimentally, one only knows that the result becomes exact with infinitely small elements. Otherwise, we get an approximation. Because only surface values of pressure and velocity are to be integrated, the mesh needs to be of two dimensions only [4].
Subdomain Modeling
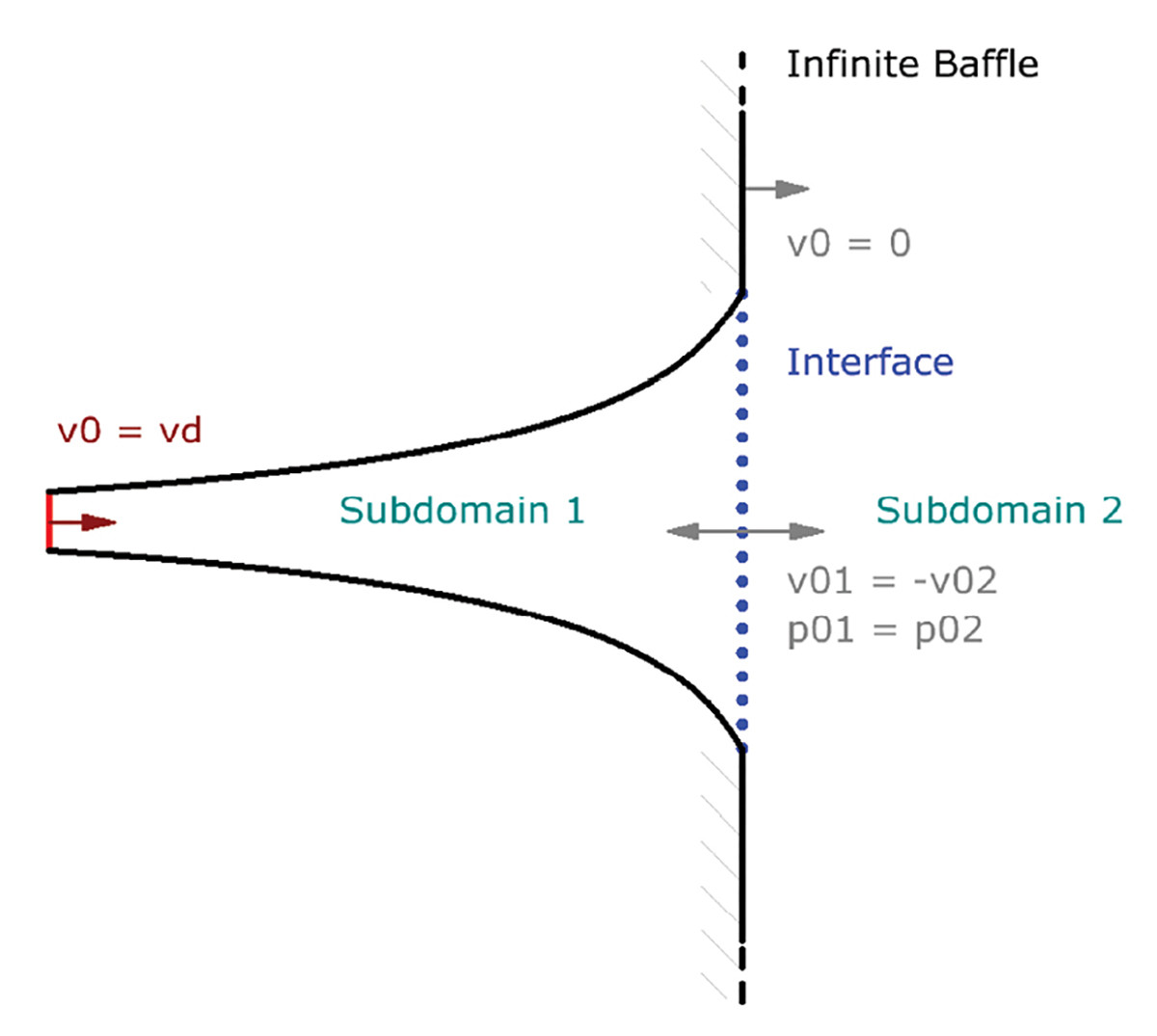
There exists a special Green-function, which automatically satisfies the condition of zero normal velocity on the infinite baffle plane. Hence, there is no need to mesh this boundary. However, this function would be valid only for boundary elements that are in or in front of the baffle.
If there are acoustic boundaries behind the infinite baffle the calculation of the acoustic field becomes more complicated. As our horn ends in the plane of the baffle, all walls of the horn are behind the infinite baffle. The trick consists of dividing the radiation domain into two subdomains as sketched in Figure 10. In between, one creates an interface where at any point there is guaranteed a continuity of parameters. The interface is acoustically transparent. On its surface the pressure of subdomain 1 is equal to the surface pressure of subdomain 2. Likewise, should the acoustic velocity be equal. Here we consider the velocity-component normal to the plane of the interface. The negative sign comes in because one regards the vectors pointing into the subdomain.
Driving
The specified boundary condition is concerned only with the surface velocity. The reflecting boundaries feature a zero normal velocity. However, the cross-section at the throat of the horn has an imprinted velocity. This motion is specified here to be uniformly distributed and simply of value one, as labeled in Figure 10 by velocity vd. The surface pressure is the parameter of solving.
Meshing
The geometry of the acoustic boundary is meshed with the help of GMSH [4], which is an external meshing tool specialized for producing elements for the boundary and finite element analysis. Only a 2D-mesh needs to be produced as we consider only the surface. The imported mesh is then refined by AKABAK to make sure all elements are smaller than a specified edge length. For the shown simulation a mesh of 1906 triangles was used for the boundaries of the horn and 1040 for the interface. We assume a constant pressure over each element. Experimentation of varying the mesh-density showed that results could be regarded sufficiently accurate up to a frequency of 10kHz.
PAFEC
Two modeling strategies were employed to analyze the baffled horn in the PAFEC VibroAcoustics software [5].
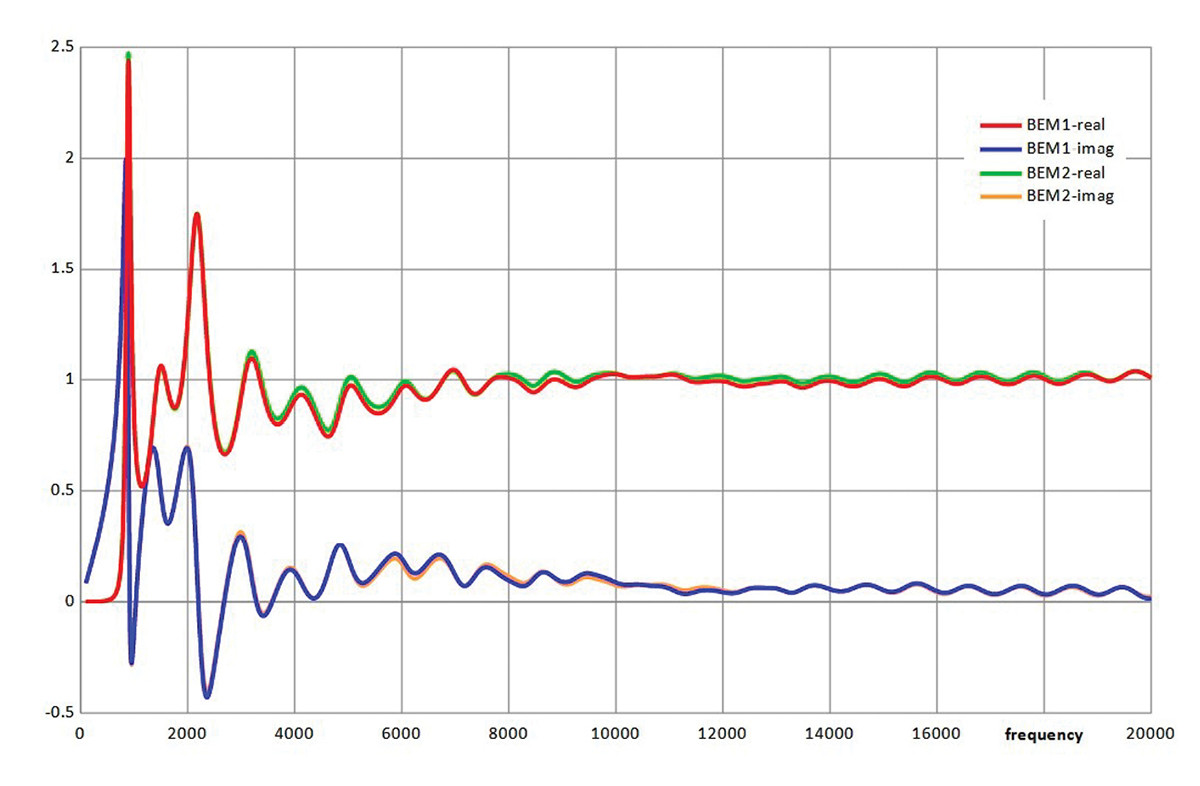
In the first approach the subdomain splitting of Figure 9a was used with 10-noded quadratic tetrahedral acoustic finite elements used in subdomain 1 and a Rayleigh integral boundary element composed of six noded quadratic triangles. The model BEM1 had 55096 acoustic finite element degrees of freedom and 2453 acoustic boundary element degrees of freedom. Based on a criterion of three quadratic elements/wavelength should be valid up to 20kHz, however because of the small radius of curvature on the “fold,” the size of elements may perhaps not have adequately represented the geometry. In many situations, where there is no constricted geometry, deviations by distances small compared with the acoustic wavelength should not significantly affect the results. To confirm this, a finer mesh density model BEM2 was run. This had 339045 acoustic finite element degrees of freedom and 9212 boundary element degrees of freedom, should be valid to 40kHz and was much closer to the geometry in the problematic area of the sharp fold near to the throat. Figure 11 compares the throat impedance for the two models. The agreement is good.
In the second approach the subdomain splitting was as in Figure 9b. Acoustic finite elements were used in subdomain 1 extending from the throat to a hemispherical surface and wave envelope elements were used in subdomain 2 for the remainder of the half space. Wave envelope elements are similar to finite elements but extend out to infinity. The basic functions are outward traveling waves, monopole, dipole, and the like. A wave envelope element-based approach can be faster than a BEM-based approach, but the accuracy is affected by the radius of the spherical surface at the interface between the subdomains and the number of terms used for outward traveling waves (= radial order). Model WEE1 had the hemispherical surface extending out to 0.072m and had radial order 2 and a total of 173915 acoustic degrees of freedom. Model WEE2 had a hemispherical radius of 0.102 m, radial order 6 and a total of 229368 acoustic degrees of freedom. Both meshes were valid to 20kHz, based on the three quadratic elements/wavelength criterion. Figure 12 compares throat impedances for WEE1 and WEE2.
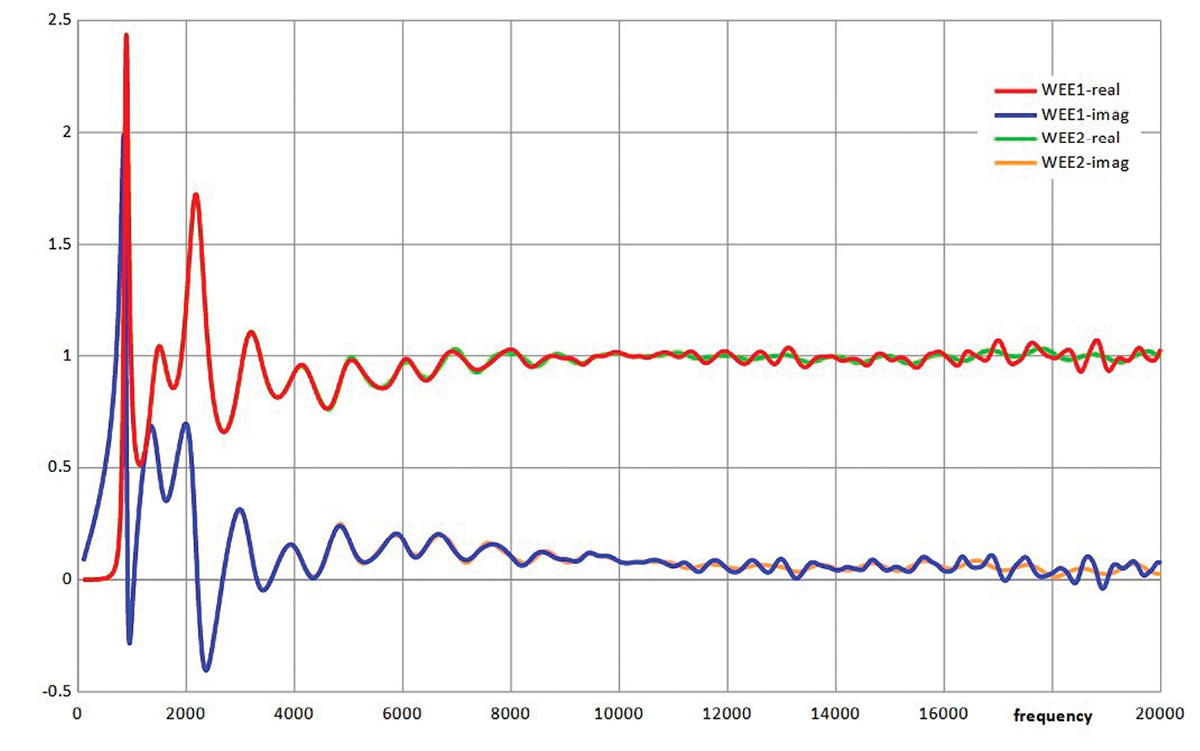
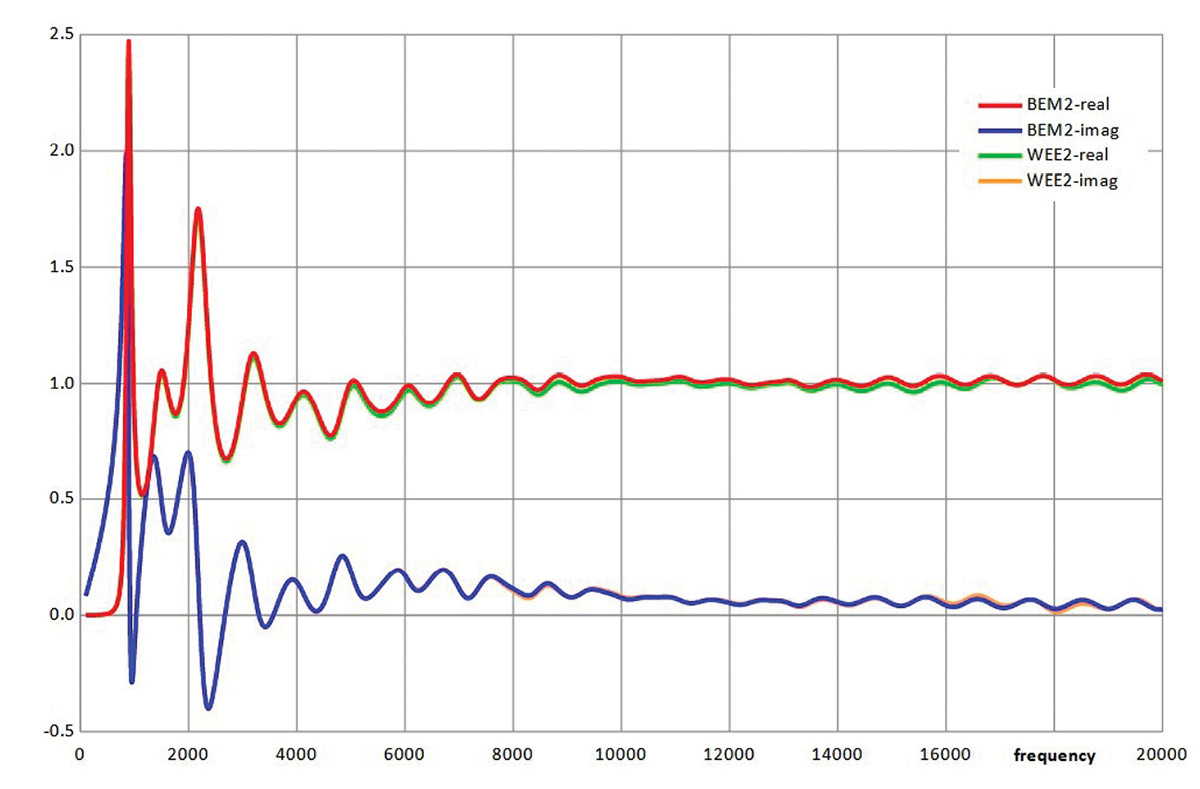
Figure 13 compares the models BEM2 and WEE2. The model WEE1 becomes less accurate at higher frequencies. It is concluded that a wave envelope element approach can produce accurate results up to high frequency, but it is necessary to take care with the hemispherical radius and radial order.
Further Work
We would like to extend the work to model the electro-dynamic compression driver so we can compare absolute sound pressure values of measurement and simulation. In that scenario AKABAK would model the compression driver with the help of the lumped element method whereas PAFEC would use the finite element method as a modeling algorithm.
Author Acknowledgements: We would like to thank Remi Vaucher for providing the horn design. Patrick Macey also gratefully acknowledges the assistance of his colleague John King for doing some of the model preparation work [6].
References
[1] N. Atalla and F. Sgard, Finite Element and Boundary Methods in Structural Acoustics and Vibration, CRC Press, 2017.
[2] S. Marburg and B. Nolte, Computational Acoustics of Noise Propagation in Fluids: Finite and Boundary Element Methods, Springer 2008.
[3] AKABAK software simulation tool, www.randteam.de
[4] GMSH, software for 2D and 3D meshing, www.gmsh.info.
[5] PAFEC level 8.8, Acoustics manual, Strelley Hall, Nottingham, UK, available upon request.
[6] The paper on which this article is based was originally presented at IOA Reproduced Sound, November 2023.
This article was originally published in audioXpress, October 2024
About the Authors
Joerg Panzer studied electrical engineering at the Technical University of Munich. He has always been active in the field of
electroacoustics and has written scientific books and papers. Joerg is the author of several widely used software applications, such as AKABAK and VACS. He teaches electroacoustics at the University of Le Mans. Joerg manages his company, which specializes in the development of industrial software applications. One of his main interests is the boundary element method.
Patrick Macey studied mathematics, graduating with a BA and a MMATH from University of Cambridge. At University of Nottingham, he obtained a PhD, “Acoustic and structure interaction problems using finite and boundary elements.” He is a fellow of the IoA. His interests include numerical techniques for vibroacoustics such as FEM, BEM, wave envelope elements, PML, series solutions and hybrid techniques, applied to electroacoustics and underwater acoustics. At PACSYS he works on development of PAFEC, PafLS and Roomcalc.
Source link
